Estimating Value at Risk using Python
Measures of exposure to financial risk

Overview

Value at risk (VaR) is a measure of market risk used in the finance, banking and insurance industries. It involves the use of statistical analysis of historical market trends and volatilities to estimate the likelihood that a given portfolio’s losses will exceed a certain amount. It is widely used for risk management and risk limit setting.

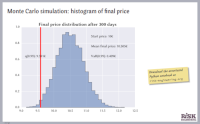
We will examine how to estimate VaR using Monte Carlo simulation techniques (also called stochastic simulation methods), analyze the effect of portfolio diversification and correlation between stocks on financial risk, and use copula methods to sample from correlated random variables and estimate portfolio VaR.

This submodule is a part of the risk analysis module.

Learning objectives

Upon completion of this module, you should be able to:

• Understand how financial risk is modeled, characterized and quantified

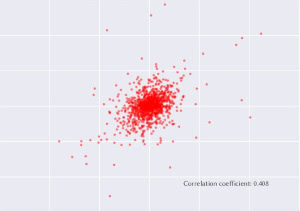
• Understand the impact of correlated risks on risk metrics

• Implement a Monte Carlo simulation procedure for stochastic estimation of some poorly-known quantity

Course material

	Estimating Value at Risk Lecture slides (PDF)
	Python notebook on analyzing risk of a stock market portfolio View Python notebook online Download Python notebook Run notebook in MyBinder Run notebook in Google Colab

In these course materials, applications are presented using the NumPy, SciPy and statsmodels libraries for the Python programming language. We have some material on getting started with Python that explains how to install Python on your computer or try out our computational notebooks using free online services.

After reading this material, you may be interested in the submodule on copula methods for representing multivariate dependencies.

Other resources

We recommend the following sources of further information on this topic:

• The Coursera course Financial Engineering and Risk Management (Columbia University)

• Video lecture Value at Risk models from MIT’s Topics in Mathematics with Applications in Finance undergrad course

• An Introduction to Computational Finance Without Agonizing Pain, by Peter Forsyth (UWaterloo), gives much more detail on Monte Carlo methods than the brief overview provided here

• Material for the Introduction to Computational Finance and Financial Econometrics course at University of Washington (Prof. E. Zivot), covering time series concepts, maximum likelihood estimation, portfolio theory and the capital asset pricing model