Monte Carlo methods for risk analysis
Stochastic simulation and numerical experiments
Overview
Some problems in risk analysis cannot be expressed in an
analytical form. Others are difficult to define in a deterministic
manner. Monte Carlo methods (also known as stochastic simulation
techniques) consist of running “numerical experiments” to observe
what happens “on average” over a large number of runs of a stochastic
model. They involve repeated random sampling from input probability
distributions, execution of the model with these stochastic inputs, then
aggregation of the large number of executions to obtain an estimate of
the quantity of interest. In some cases Monte Carlo methods are a simple
and convenient alternative to analytical methods, allowing you to
express your problem in a direct way and let the computer do the hard
work. For complex problems which cannot be resolved analytically, they
may be the only way of estimating the output of interest. These methods
rely on the speed of modern computers and their ability to generate
pseudo-random numbers from various relevant probability
distributions.
Monte Carlo methods are widely used in risk analysis, for instance for:
propagating uncertainty through a numerical model to obtain confidence intervals on your model outputs
estimating quantile measures for performance measures
simulating evacuation from a building during the design phase
predicting failure, cost overruns and schedule overruns in project management
This submodule is a part of the risk analysis module.
Course material
 |
Monte Carlo methods in risk analysis |
 |
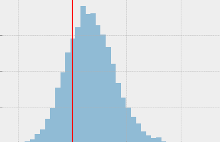
Estimating pi using a Monte Carlo simulation |
 |
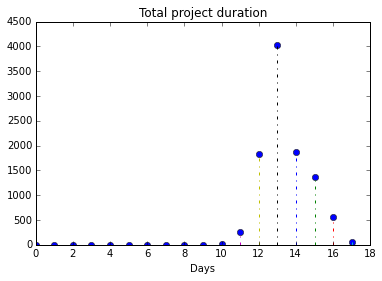Project risk analysis with Monte Carlo simulation |
 |
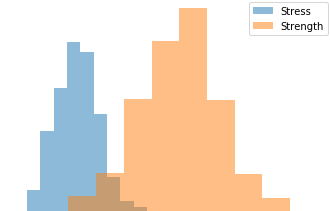Monte Carlo simulation of failure probability in mechanical design |
 |
Estimating failure probability of a space vessel fuel tank |
|
Estimating failure probability of a space vessel fuel tank (Rust kernel) |
 |
Monte Carlo simulation of landslide risk |
 |
Numerical integration using Monte Carlo methods |
 |
Monte Carlo sampling methods |
 |
Limits of stochastic simulation methods: the Saint Petersburg problem |
 |
Various poker odds: working with discrete probability distributions |
In these course materials, applications are presented using the NumPy, SciPy and statsmodels libraries for the Python programming language. We have some material on getting started with Python that explains how to install Python on your computer or try out our computational notebooks using free online services.
One of the notebooks above shows how to implement Monte Carlo sampling in a notebook-style interactive environment with the high-performance Rust programming language, which will typically be many thousands of times faster than implementations in Python. We also include links to relevant plugins for Microsoft Excel, if you’re into that kind of thing.
One of the Python notebooks above illustrates alternative methods to standard (naïve) random sampling:
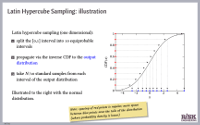
Latin Hypercube Sampling (LHS) or stratified sampling without replacement involves splitting up each input variable into a number of equiprobable intervals and sampling separately from each interval, using the inverse cumulative distribution function for that variable. In typically leads to faster convergence than Monte Carlo procedures that implement standard random sampling.
Low-discrepancy sequences or quasi-random sequences such as the Halton and Sobol’ sequences, which fill the input space more quickly than pseudorandom sequences and typically lead to faster convergence than standard random sampling. These are based on deterministic mathematical sequences of points that don’t “cluster” together.
The notebook on stochastic simulation of the Saint Petersburg problem linked to above illustrates a situation where very unlikely events have an extremely high impact on the mean outcome. In such situations, Monte Carlo simulation is not a good approach to estimate the output of interest (expected value of playing the game, in this case).
Other resources
We recommend the following sources of further information on this topic:
The Harvard AM207 course on stochastic methods for data analysis, inference and optimization
MIT OpenCourseWare notes from the Numerical computation for mechanical engineers course
Article Principles of Good Practice for the use of Monte Carlo Techniques, Risk Analysis, 1994
Book The Monte Carlo Simulation Method for System Reliability and Risk Analysis, Enrico Zio
An alternative geometrical method to estimate the value of pi using stochastic sampling is Buffon’s Needle, invented in 1777. For more on the history of Monte Carlo computational methods, read this article from LANL magazine Actinide.
Published:
Last updated: