Statistical modelling
Introduction to probabilistic and statistical modelling of risk
Overview
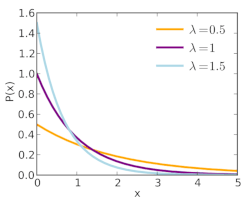Risk analysis is sometimes based on the
analysis of data concerning a hazardous event, such as
the occurrence of an earthquake, or the exceedance of a threshold. This
analysis is based on statistical modelling, most often with computer
tools. When the risk analyst puts her data scientist hat on, she
collects data (measurements, observations) from various sources and
inputs them into the computer, obtains a general overview of the data
and its distribution, and builds a statistical model which attempts to
reproduce properties of the underlying phenomena. After checking that
the statistical model is a good fit for the observations, she can
generate various risk metrics and quantify the
level of uncertainty in the predictions.
Statistical modelling (or “data science” or “machine learning”, to use related and more trendy terms) is an important part of risk analysis and safety in various engineering areas (mechanical engineering, nuclear engineering), in the management of natural hazards, in quality control, and in finance.
This submodule is a part of the risk analysis module.
Learning objectives
Upon completion of this submodule, you should be able to:
Analyze data using descriptive statistics and graphical tools
Fit a probability distribution to data (estimate distribution parameters)
Express various risk measures as statistical tests
Determine quantile measures of various risk metrics
Build flexible models to allow estimation of quantities of interest and associated uncertainty measures
Select appropriate distributions of random variables/vectors for random phenomena
Course material
 |
Statistics and risk modelling with Python |
 |
Python notebook on basic statistics |
 |
Python notebook on coins and dice |
 |
Python notebook on probability distributions |
 |
Brief reminder on statistics |
 |
Analyzing data with Python |
 |
Exercise (Python notebook) on descriptive statistics |
|
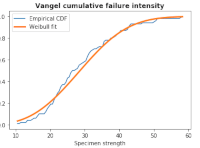
Python notebook on simple descriptive statistics |
 |
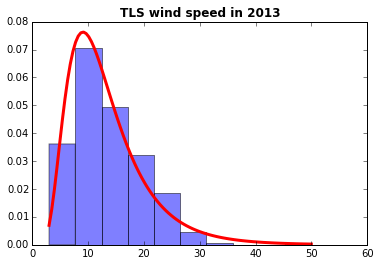Python notebook on analysis and curve fitting for weather data |
 |
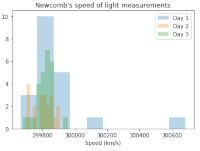Python notebook on analysis of speed of light measurements |
 |
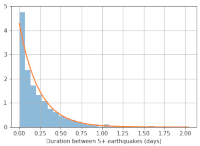Python notebook on analysis of earthquake data |
 |
Python notebook on Semmelweis’s work on risk reduction in hospitals |
 |
Python notebook on intervention analysis using a hierarchical model |
In these course materials, applications are presented using the NumPy, SciPy and statsmodels libraries for the Python programming language. We have some material on getting started with Python that explains how to install Python on your computer or try out our computational notebooks using free online services.
Other resources
We recommend the following sources of further information on this topic:
CMU Open Learning Initiative course Probability and Statistics, a free and open (course materials can be followed at any time) course
Seeing theory, a very nice visual introduction to basic concepts in probability and statistics from Brown University
Course materials for the MIT Introduction to Probability and Statistics course, which is free and open (course materials can be followed at any time)
Course materials for Harvard’s Introduction to Data Science (CS109a) course
EdX course Probability - The Science of Uncertainty and Data (MITx) – note that the course can only be taken at specific periods during the year
Udacity course Introduction to statistics (no prerequisites, but note that the course can only be taken at specific periods during the year)
Textbook Introduction to Probability by C. Grinstead and J. L. Snell, freely available under GNU Free Documentation Licence
Textbook Statistical inference for everyone, freely available under a Creative Commons licence
Computational statistics in Python, an online textbook with many examples
Python for econometrics (University of Oxford, UK)
Exploratory computing with Python, a set of Python notebooks on analyzing data using NumPy/SciPy
Book: Statistical modeling: a fresh approach by Daniel Kaplan
The Probability and statistics cookbook, by Matthias Vallentin
The NIST Engineering Statistics Handbook, an online compendium of information on statistics useful for engineering analysis
Back to top
Published:
Last updated: